Cryptographic Keys

RSA Keys

Summary

RSA (Rivest Shamir Adleman) has been the standard for asymmetric cryptography for 3 decades. RSA uses the prime factorization method for one-way encryption of a message. While certain attacks have been found due to poorly implemented random number generation, this method has passed the test of time by being a trusted cryptographic method for over 3 decades with no significant findings. While the algorithm is very secure, with the advances on compute, factorizing large numbers has become easier for large computers, forcing the industry to move from 512 bit keys, to 1024 bit keys, and now 2048 bit keys and some governments recommending 4096 bit keys.

Since the RSA algorithm has been the standard since the 90s, most computers will be capable of encrypting and decrypting data using RSA. Making RSA the perfect default cryptographic algorithm for new PKI implementations that must be compatible with older devices or IoT devices that might not have ECC capabilities.

Mathematical Overview

In this method, two large prime numbers are multiplied together to create a larger number. This makes it very easy to create the large number but very hard to find the two prime numbers that created the number. Learn more about the mathematics behind RSA. If the mathematics for cryptography excite you, also check our careers page.

ECDSA Elliptic Curve Digital Signature Algorithm

Summary

ECDSA (Elliptic Curve Digital Signature Algorithm) was standardized in 2005. Due to its ability to use smaller keys to achieve the same security as RSA, it makes it a faster and more efficient algorithm. However, due to its complexity and relatively shorter age, ECDSA has not been widely adopted by the web community. Meaning that if your PKI needs to be validated by older devices/browsers you might run into compatibility issues and would better off with RSA. However, if you do not have that restriction we highly recommend using ECDSA for more efficient cryptographic operations.

Mathematical Overview

It is hard to explain ECDSA mathematics without getting very deep into the mathematics behind elliptic curves over finite fields. For sake of simplicity, we will say that ECDSA works by having a mathematical equation which draws a curve on a graph, then the computer chooses a random point on that curve. This is your private key. Then some mathematical magic using the curve and your origin point creates the public key. The computational complexity of this discrete log problem allows ECDSA to achieve the same level of security as RSA with significantly smaller keys. Learn more about the mathematics behind ECDSA. If the mathematics for cryptography excite you, also check our careers page.

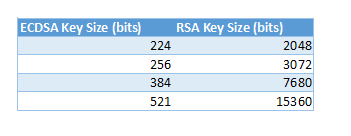
RSA vs ECDSA Key Size Comparison

As mentioned in the ECDSA section, ECDSA can achieve the same level of theoretical security with smaller keys. The table bellow shows the equivalent key size for each algorithm.